고정 헤더 영역
상세 컨텐츠
본문
서로소 집합
공통 원소가 없는 두 집합을 의미한다.
서로소 집합 자료구조란 서로소 부분 집합을로 나누어진 원소들의 데이터를 처리하기 위한 자료구조이다.
1. union(합집합) 연산을 확인하여, 서로 연결된 두 노드 A, B를 확인한다.
I. A와 B의 루트 노드 A', B'를 각각 찾는다.
II. A'를 B'의 부모 노드로 설정한다(B'가 A'를 가리키도록 한다.)
2. 모든 union(합집합) 연산을 처리할 때까지 1번 과정을 반복한다.
Step 0. 초기 단계에서는 가장 먼저 노드의 개수(V) 크기의 부모 테이블을 초기화한다. 이때 모든 원소가 자기 자신을 부모로 가지도록 설정한다. 현재 원소의 개수가 6이므로, 초기 단계에서는 총 6개의 트리가 존재하는 것과 같다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 부모 | 1 | 2 | 3 | 4 | 5 | 6 |
Step 1. union1, 4
첫 번째 union 연산을 확인하면 1과 4를 합친다. 이때는 노드 1과 노드4의 루트 노드를 각각 찾으면 된다. 현재 루트 노드는 각각 1과 4이기 때문에 더 큰 번호에 해당하는 루트 노드 4의 부모를 1로 설정한다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 부모 | 1 | 2 | 3 | 1 | 5 | 6 |
Step 2. union2, 3
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 부모 | 1 | 2 | 2 | 1 | 5 | 6 |
Step3. union 2, 4
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 부모 | 1 | 1 | 2 | 1 | 5 | 6 |
Step4. union 5, 6
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 부모 | 1 | 1 | 2 | 1 | 5 | 5 |
위 과정을 소스로 구현해보자.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
return find_parent(parent, parent[x])
return x
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
parent[i] = i
# union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
# 각 원소가 속한 집합 출력
print('각 원소가 속한 집합: ', end='')
for i in range(1, v+1):
print(find_parent(parent, i), end = ' ')
print()
# 부모 테이블 내용 출력
print('부모 테이블: ', end ='')
for i in range(1, v+1):
print(parent[i], end = ' ')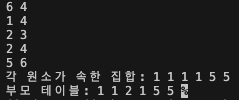
위 코드에서 예시를 들면 노드 5의 루트를 찾기 위해서는 노드5->노드4->노드3->노드2->노드1 순서대로 부모 노드를 거슬러 올라가야하므로 최대 O(V)의 시간이 소요될 수 있다.
결과적으로 현재의 알고리즘을 그대로 이용하게 되면 노드의 개수가 V개이고 find 혹은 union 연산의 개수가 M개일 때, 전체 시간 복잡도는 O(VM)이 되어 비효율적이다.
이러한 점을 개선시킬 수 있는 압축기법 소스코드가 있다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x]
return parent[x]각 노드에 대하여 find함수를 호출한 이후에, 해당 노드의 루트 노드가 바로 부모 노드가 된다.
경로 압축 기법을 이용하게 되면 루트 노드에 더욱 빠르게 접근할 수 있다는 점에서 기존의 기본적인 알고리즘과 비교했을 때 시간 복잡도가 개선된다.
# # 특정 원소가 속한 집합을 찾기
# def find_parent(parent, x):
# # 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
# if parent[x] != x:
# return find_parent(parent, parent[x])
# return x
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
parent[i] = i
# union 연산을 각각 수행
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
# 각 원소가 속한 집합 출력
print('각 원소가 속한 집합: ', end='')
for i in range(1, v+1):
print(find_parent(parent, i), end = ' ')
print()
# 부모 테이블 내용 출력
print('부모 테이블: ', end ='')
for i in range(1, v+1):
print(parent[i], end = ' ')
개선된 방식의 시간 복잡도를 알아보자.
노드의 개수가 V개이고, 최대 V-1개의 union 연산과 M개의 find연산이 가능할 때 경로 압축 방법을 적용한 시간 복잡도는 O(V+M(1+log(2-M/V)V))라는 것이 알려져 있다.
대략 V + Mlog2V를 계산한다.
서로소 집합을 활용한 사이클 판별
서로소 집합은 다양한 알고리즘에 사용될 수 있다.
특히 서로소 집합은 무방향 그래프 내에서의 사이클을 판별할 때 사용할 수 있다는 특징이 있다.
참고로 방향 그래프에서의 사이클 여부는 DFS를 이용하여 판별 할 수 있다.
앞서 union 연산은 그래프에서의 간선으로 표현될 수 있다고 했다.
따라서 간선을 하나씩 확인하면서 두 노드가 포함되어 있는 집합을 합치는 과정을 반복하는 것만으로도 사이클을 판별할 수 있다.
1. 각 간선을 확인하며 두 노드의 루트 노드를 확인한다.
I. 루트 노드가 서로 다르다면 두 노드에 대하여 union 연산을 수행한다.
II. 루트 노드가 서로 같다면 사이클(Cycle)이 발생한것이다.
2. 그래프에 포함되어 있는 모든 간선에 대하여 1번 과정을 반복한다.
Step 0. 초기 단계에서는 모든 노드에 대하여 자기 자신을 부모로 설정하는 형태로 부모 테이블을 초기화한다.
| 인덱스 | 1 | 2 | 3 |
| 부모 | 1 | 2 | 3 |
Step 1. 가장 먼저 간선 (1, 2)를 확인한다. 노드 1과 노드 2의 루트 노드는 각각 1과 2이다. 따라서 더 큰 번호를 갖는 노드 2의 부모 노드를 1로 변경한다.
| 인덱스 | 1 | 2 | 3 |
| 부모 | 1 | 1 | 3 |
Step 2. 간선 (1, 3)을 확인한다. 노드 1과 노드 3의 루트 노드는 각각 1과 3이다. 따라서 더 큰 번호를 갖는 노드 3의 부모 노드를 1로 변경한다.
| 인덱스 | 1 | 2 | 3 |
| 부모 | 1 | 1 | 1 |
Step3. 이후에 (2, 3) 간선을 확인한다. 다만, 이때 노드 2와 노드 3이 이미 루트 노드로 '노드 1'을 가지고 있다. 다시 말해서 사이클이 발생한다는 것을 알 수 있다.
책에서 구현한 코드이다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
parent[i] = i
cycle = False # 사이클 발생 여부
for i in range(e):
a, b = map(int, input().split())
# 사이클이 발생한 경우 종료
if find_parent(parent, a) == find_parent(parent, b):
cycle = True
break
# 사이클이 발생하지 않았다면 합집합(union) 수행
else:
union_parent(parent, a, b)
if cycle:
print("사이클이 발생했습니다.")
else:
print("사이클이 발생하지 않았습니다.")
신장트리
하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다.
조건은 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건인데, 트립의 성립 조건이기도 하다.
그래서 신장트리라고 하고 아래와 같다.
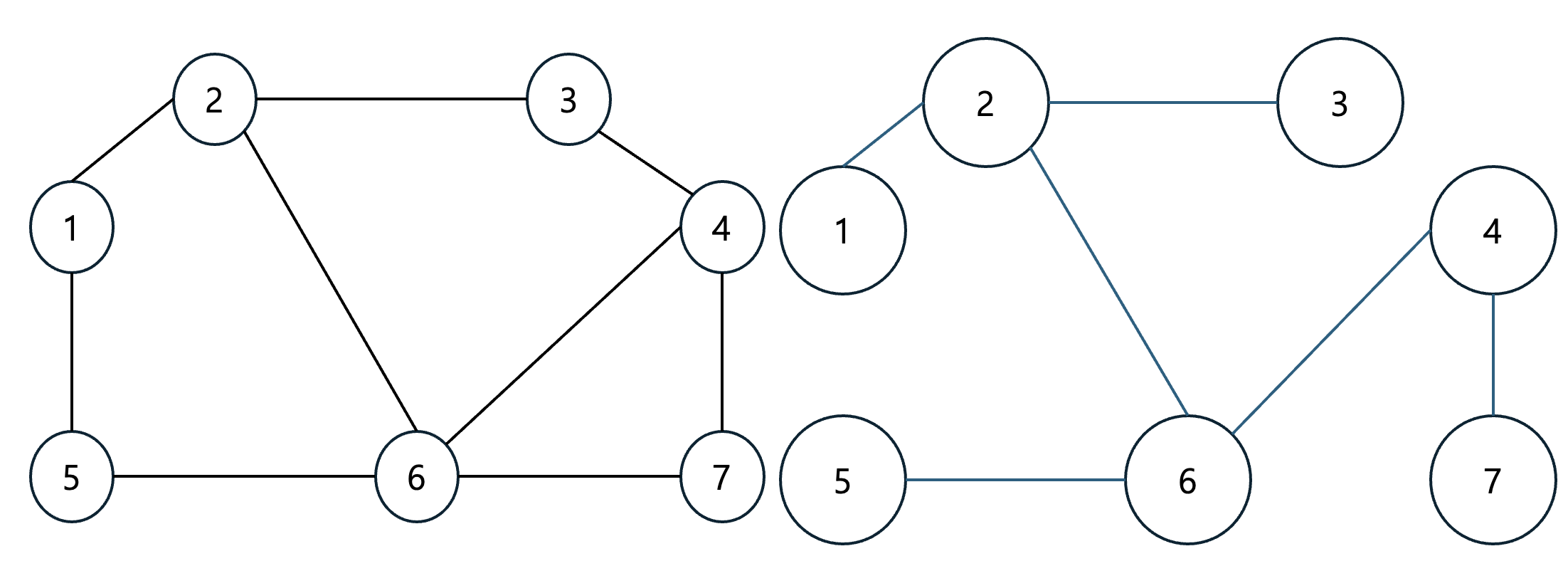
왼쪽의 그래프에서 오른쪽과 같은 신장트리를 여러개 찾을 수 있다.

위의 그래프는 노드1을 포함하고 있지 않기에 신장 트리에 해당하지 않는다.
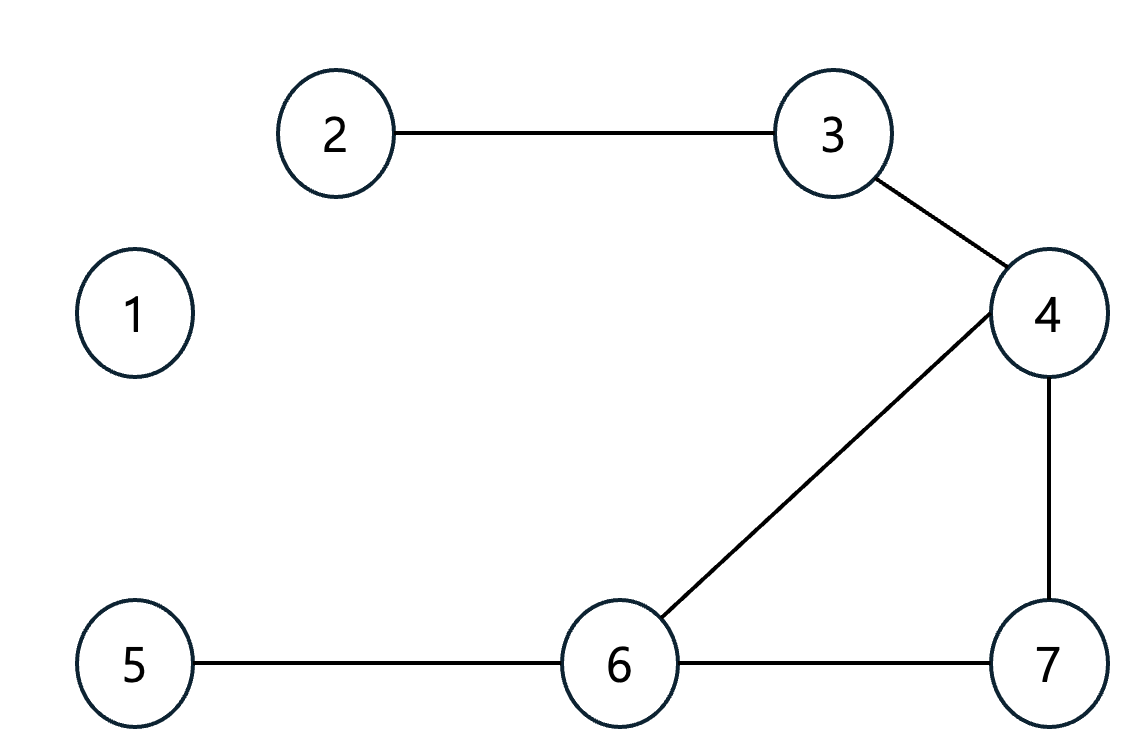
위의 그래프는 사이클이 존재하므로 신장 트리가 아니다.
크루스칼 알고리즘
우리는 최소한의 비용으로 신장트리를 찾아야 할 때가 있다.
예를 들어 N개의 도시가 존재하는 상황에서 두 도시 사이에 도로를 놓아 전체 도시가 서로 연결될 수 있게 도로를 설치하는 경우이다.
이런 경우 최소 신장 트리 알고리즘(크루스칼 알고리즘(kruskal algorithm))이라고 한다.
크루스칼 알고리즘은 그리디 알고리즘으로 분류된다.
먼저 모든 간선에 대하여 정렬을 수행한 뒤에 가장 거리가 짧은 간선부터 집합에 포함시키면 된다. 이때 사이클을 발생시킬 수 있는 간선의 경우, 집합에 포함시키지 않는다. 순서는 아래와 같다.
- 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
- 사이클이 발생하지 않는 경우 최소 신장 트리에 포함시킨다.
- 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다.
- 모든 간선에 대하여 2번의 과정을 반복한다.
아래 그래프의 최소 신장 트리를 구해보자.
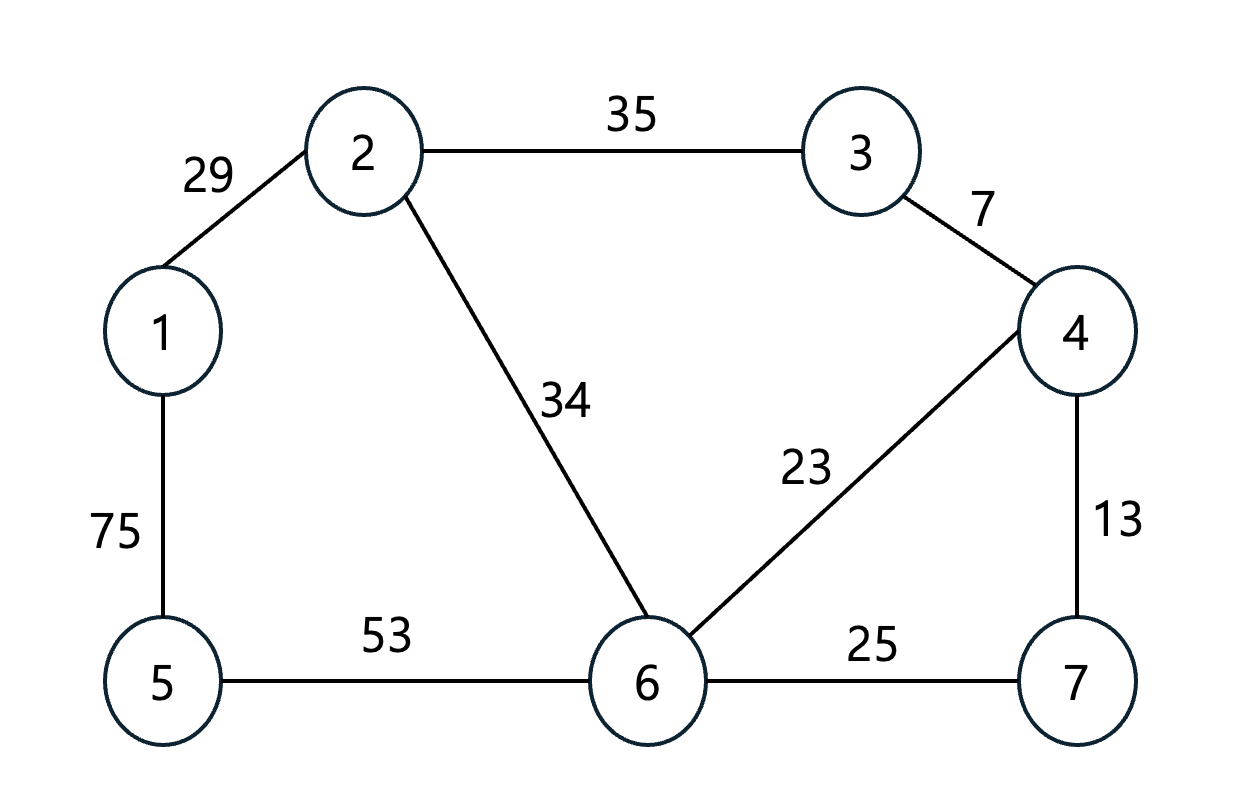
신장 트리는 트리 자료구조이므로, 최종적으로 신장 트리에 포함되는 간선의 개수가 노드의 개수 -1과 같다.
노드의 개수는 7이고, 간선의 개수가 6개이다.
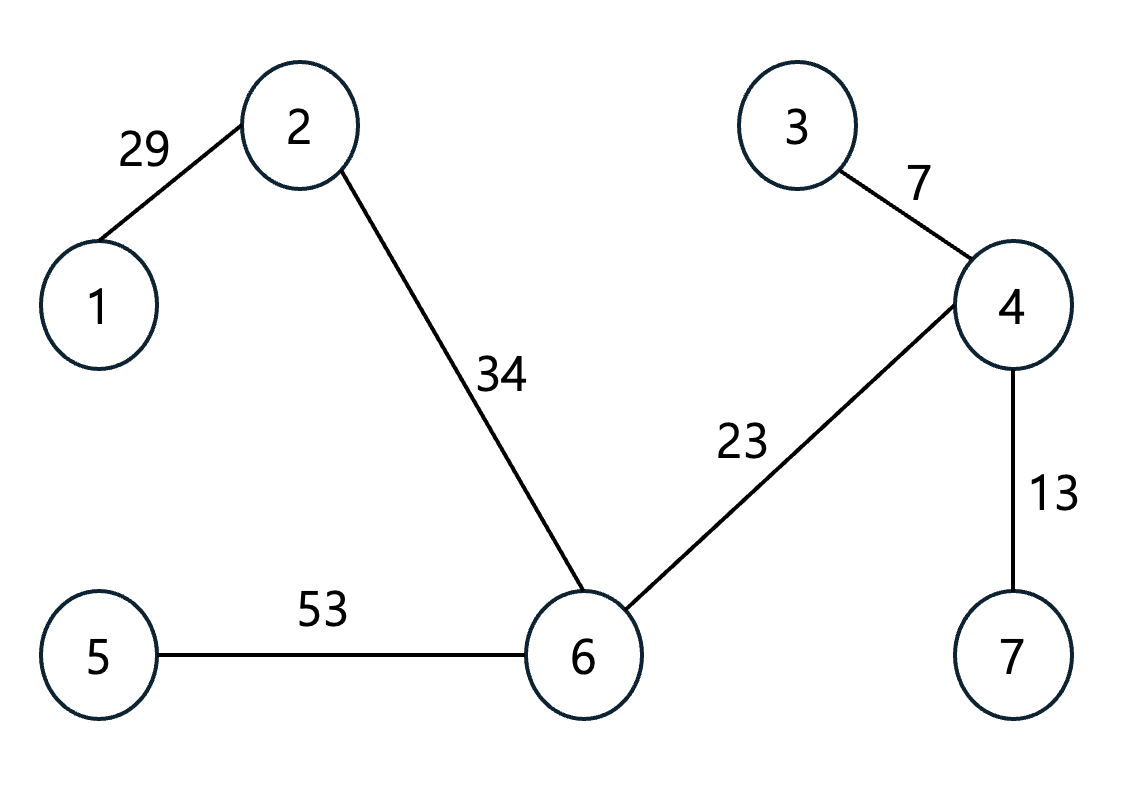
이제 가장 거리가 짧은 간선부터 차례대로 집합에 추가하면 된다는 것이다. 다만, 사이클을 발생시키는 간선은 제외하고 연결한다.
이렇게 하면 항상 최적의 해를 보장할 수 있다.
단계별로 알아보자.
Step 0. 초기 단계에서는 그래프의 모든 간선 정보만 따로 빼내어 정렬을 수행한다. 현재 전체 그래프에 존재하는 간선이 9개인 것을 알 수 있다. 따라서 맨 처음에는 모든 간선을 정렬.

| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
Step 1. 첫 번째 단계에서는 가장 짧은 간선을 선택한다. 따라서 (3, 4)가 선택되고 이것을 집합에 포함.(노드 3과 4를 union)
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 1 |
Step 2. 그 다음으로 비용이 가장 작은 간선인(4, 7)을 선택한다. 현재 노드4와 노드7은 같은 집합에 속해 있지 않기에 union.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 1 | Step 2 |
Step 3. 가장 적은 간선인 (4, 6)을 선택한다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 1 | Step 3 | Step 2 |
Step 4. 가장 적은 간선인(6, 7)을 선택한다. 하지만 노드6과 노드7은 이미 동일한 집합에 포함되어 있으므로 union X
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 1 | Step 3 | Step 2 | Step 4 |
Step 5. 가장 적은 간선(1, 2)를 선택한다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 5 | Step 1 | Step 3 | Step 2 | Step 4 |
Step 6. 가장 적은 간선(2 ,6)을 선택(다른 집합이여서 가능)
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 5 | Step 6 | Step 1 | Step 3 | Step 2 | Step 4 |
Step 7. 가장 적은 간선(2, 3)을 선택한다. 동일 집합이라 X
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 5 | Step 7 | Step 6 | Step 1 | Step 3 | Step 2 | Step 4 |
Step 8. 가장 적은 간선(5, 6)을 선택한다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 5 | Step 7 | Step 6 | Step 1 | Step 3 | Step 2 | Step 8 | Step 4 |
Step 9. 가장 적은 간선(1, 5)을 선택한다. 동일 집합이라 X
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | Step 5 | Step 9 | Step 7 | Step 6 | Step 1 | Step 3 | Step 2 | Step 8 | Step 4 |
총 비용은 159이고, 책에서 코드로 구현한 예시이다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화
# 모든 간선을 담을 리스트와 최종 비용을 담은 변수
edges = []
result = 0
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v+1):
parent[i] = i
# 모든 간선에 대한 정보를 입력받기
for _ in range(e):
a, b, cost = map(int, input().split())
# 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
edges.append((cost, a, b))
# 간선을 비용순으로 정렬
edges.sort()
# 간선을 하나씩 확인하며
for edge in edges:
cost, a, b = edge
# 사이클이 발생하지 않는 경우에만 집합에 포함
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result += cost
print(result)
크루스칼 알고리즘의 시간 복잡도는
간선의 개수가 E일때, O(ElogE)의 시간 복잡도를 가진다.
간섭을 정렬하는 작업이 제일 오래 걸리며, E개의 데이터를 정렬했을 때의 시간 복잡도는 O(ElogE)이기 때문이다.
union과정은 정렬보다 시간 복잡도가 작으므로 무시한다.
위상정렬
방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것이다.
방법은 아래와 같다.
- 진입차수가 0인 노드를 큐에 넣는다.
- 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
바로 그림으로 살펴보자.
Step 0. 초기 단계에서는 진입차수가 0인 노드를 큐에 넣는다. 현재 노드1의 진입차수만 0이기 때문에 큐에 노드 1만 삽입한다.
현재 노드 1의 진입차수가 0이기 때문에 큐에 노드 1만 삽입한다. 큐에 삽입된 노드는 색을 다르게.
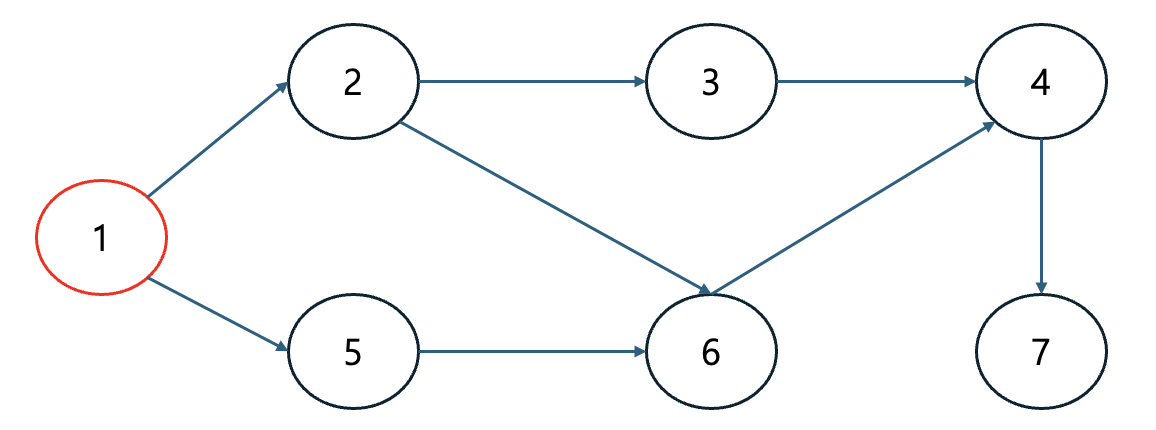
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 1 | 1 | 2 | 1 | 2 | 1 |
| 큐 | 노드 1 |
Step 1. 먼저 큐에 들어 있는 노드 1을 꺼낸다. 이제 노드 1과 연결되어 있는 간선들을 제거한다. 그러면 새롭게 노드 2와 노드 5의 진입차수가 0이 된다. 따라서 노드 2와 노드 5를 큐에 삽입한다. 처리된 노드와 간선은 지우겠다.
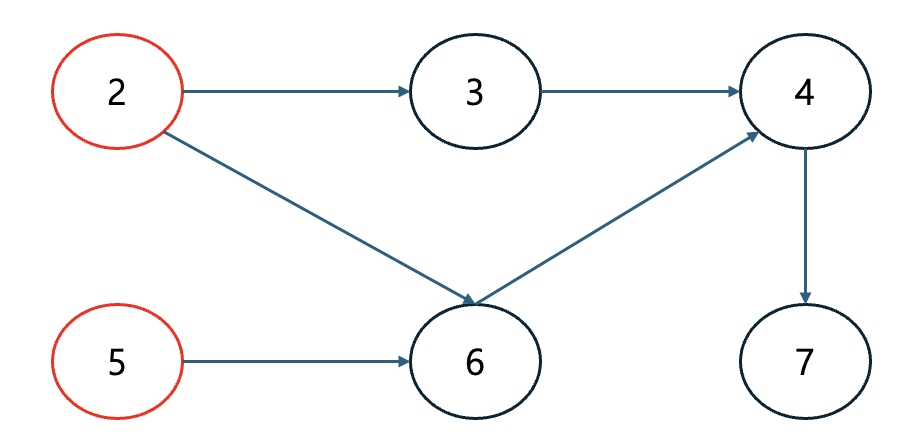
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 1 | 2 | 0 | 2 | 1 |
| 큐 | 노드 2, 노드 5 |
Step 2. 그다음 큐에 들어 있는 노드 2를 꺼낸다. 이제 노드 2와 연결되어 있는 간선들을 제거한다.
그러면 새롭게 노드 3의 진입차수가 0이 된다. 따라서 노드 3을 큐에 삽입
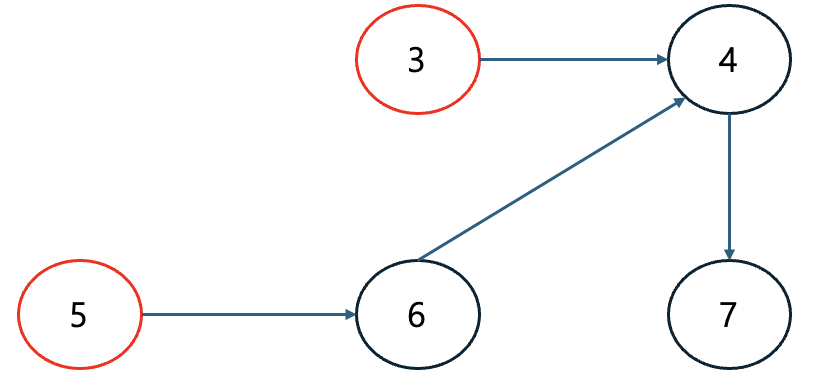
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 2 | 0 | 1 | 1 |
| 큐 | 노드 5, 노드 3 |
Step 3. 그 다음 큐에 들어있는 노드 5를 꺼낸다. 이제 노드 5와 연결되어 있는 간선들을 제거.
그러면 새롭게 노드 6의 진입차수가 0이된다. 따라서 노드 6을 큐에 삽입한다.
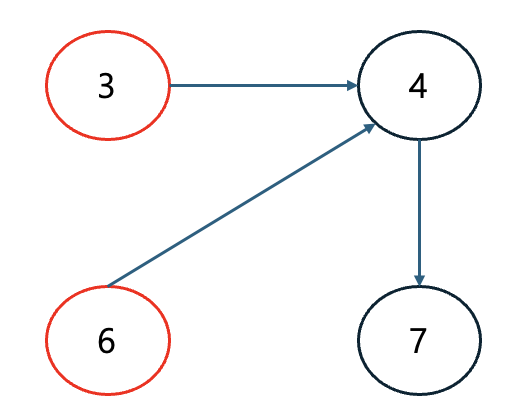
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 2 | 0 | 0 | 1 |
| 큐 | 노드 3, 노드 6 |
Step 4. 그 다음 큐에 들어 있는 노드 3을 꺼낸다. 이제 노드 3과 연결되어 있는 간선들을 제거한다.
이번 단계에서는 새롭게 진입차수가 0이 되는 노드가 없으므로 그냥 넘어간다.
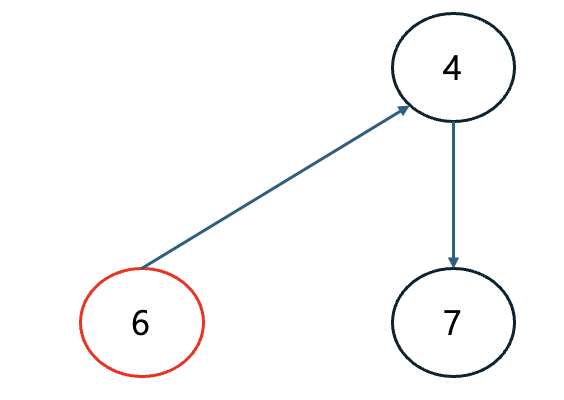
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 큐 | 노드 6 |
Step 5. 그 다음 큐에 들어 있는 노드 6을 꺼낸다. 이제 노드 6과 연결되어 있는 간선을 제거.
그러면 새롭게 노드 4의 진입차수가 0이 된다. 따라서 노드 4를 큐에 삽입.
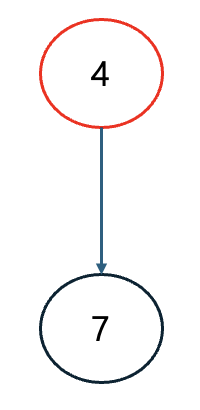
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 큐 | 노드 4 |
Step 6. 그 다음 큐에 들어 있는 노드 4를 꺼낸다. 이제 노드 4와 연결되어 있는 간선을 제거.
그러면 새롭게 노드 7의 진입차수가 0이 된다. 따라서 노드 7을 큐에 삽입한다.

| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 큐 | 노드 7 |
Step 7. 그 다음 큐에 들어있는 노드 7을 꺼내면 끝.
1 - 2 - 5 - 3 - 6 - 4 - 7
1 - 5 - 2 - 3 - 6 - 4 - 7
from collections import deque
# 노드의 개수와 간선의 개수를 입력받기
v, e = map(int, input().split())
# 모든 노드에 대한 진입차수는 0으로 초기화
indegree = [0] * (v+1)
# 각 노드에 연결된 간선 정보를 담기 위한 연결리스트(그래프) 초기화
graph = [[] for i in range(v+1)]
# 방향 그래프의 모든 간선 정보를 입력받기
for _ in range(e):
a, b = map(int, input().split())
graph[a].append(b) # 장점 A에서 B로 이동가능
# 진입차수를 1 증가
indegree[b] += 1
# 위상 정렬 함수
def topology_sort():
result = [] # 알고리즘 수행 결과를 담을 리스트
q = deque()
# 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v+1):
if indegree[i] == 0:
q.append(i)
# 큐가 빌 때까지 반복
while q:
# 큐에서 원소 꺼내기
now = q.popleft()
result.append(now)
# 해당 원소와 연결된 노드들의 진입차수에서 1빼기
for i in graph[now]:
indegree[i] -= 1
# 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if indegree[i] == 0:
q.append(i)
# 위상 정렬을 수행한 결과 출력
for i in result:
print(i, end=' ')
topology_sort()
위상 정렬의 시간복잡도는 O(V+E)이다.
위상 정렬을 수행할 때는 차례대로 모든 노드를 확인하면서, 해당 노드에서 출발하는 간선을 차례대로 제거해야한다.
결과적으로 노드와 간선을 모두 확인한다는 측면에서 O(V+E)의 시간이 소요되는 것이다.
연습문제 1. 팀 결성
학교에서 학생들에게 0번부터 N번까지의 번호를 부여했다. 처음에는 모든 학생이 서로 다른 팀으로 구분되어, 총 N + 1 개의 팀이 존재한다. 이때 선생님은 '팀 합치기' 연산과 '같은 팀 여부 확인' 연산에 대해 연산 결과를 출력하는 프로그램을 작성.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
n, m = map(int, input().split())
parent = [0] * (n + 1) # 부모 테이블 초기화
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(0, n + 1):
parent[i] = i
# 각 연산을 하나씩 확인
for i in range(m):
oper, a, b = map(int, input().split())
# 합집합 연산인 경우
if oper == 0:
union_parent(parent, a, b)
# 찾기 연산인 경우
elif oper == 1:
if find_parent(parent, a) == find_parent(parent, b):
print('YES')
else:
print('NO')
연습문제 2. 도시 분할 계획
마을은 N개의 집과 그 집들을 연결하는 M개의 길로 이루어져 있다. 길은 어느 방향으로든지 다닐 수 있는 편리한 길이다.
그리고 길마다 길을 유지하는데 드는 유지비가 있다.
마을의 이장은 마을을 2개의 분리된 마을로 분할할건데, 너무 커서 혼자 관리하지 못한다.
마을을 분할할 때는 각 분리된 마을 안에 집들이 서로 연결되도록 분할해야한다.(분리된 마을 안에 있는 두 집 사이에 경로가 항상 존재햐야하고 마을에는 집이 하나 이사 있어야한다.)
길이 너무 많아, 분리된 두 마을 사이에 있는 길들은 필요가 없어 없앨 수 있고, 각 분리된 마을 안에서도 임의의 두 집 사이에 경로가 항상 존재하게 하면서 길을 더 없앨 수 있다.
마을의 이장은 위 조건을 만족하도록 길을 없애고, 길의 유지비의 합을 최소로 하고 싶다.
# 특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
# 노드의 개수와 간선(union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [0] * (v + 1) # 부모 테이블 초기화
# 모든 간선을 담을 리스트와 최종 비용을 담을 변수
edges = []
result = 0
# 부모 테이블상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
parent[i] = i
# 모든 간선에 대한 정보를 입력받기
for _ in range(e):
a, b, cost = map(int, input().split())
# 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
edges.append((cost, a, b))
# 간선을 비용순으로 정렬
edges.sort()
last = 0 # 최소 신장 트리에 포함되는 간선 중에서 가장 비용이 큰 간선
# 간선을 하나씩 확인하며
for edge in edges:
cost, a, b = edge
# 사이클이 발생하지 않는 경우에만 집합에 포함
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
result += cost
last = cost
print(result - last)
연습문제 3. 커리큘럼
온라인 강의에는 선수 강의가 있는데, 주어진 강의를 전부 듣기 위한 최소 시간을 구하는 문제이다.
input은 첫번째 줄에는 강의수이고,
두번째 라인은 첫번째 강의의 시간을 나타내고,
세번째 라인부터는 수강시 필요한 시간과 선수강의의 index가 주어진다.
from collections import deque
import copy
# 노드의 개수 입력받기
v = int(input())
# 모든 노드에 대한 진입차수는 0으로 초기화
indegree = [0] * (v + 1)
# 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트(그래프) 초기화
graph = [[] for i in range(v + 1)]
# 각 강의 시간을 0으로 초기화
time = [0] * (v + 1)
# 방향 그래프의 모든 간선 정보를 입력받기
for i in range(1, v + 1):
data = list(map(int, input().split()))
time[i] = data[0] # 첫 번째 수는 시간 정보를 담고 있음
for x in data[1:-1]:
indegree[i] += 1
graph[x].append(i)
# 위상 정렬 함수
def topology_sort():
result = copy.deepcopy(time) # 알고리즘 수행 결과를 담을 리스트
q = deque()
# 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v + 1):
if indegree[i] == 0:
q.append(i)
# 큐가 빌 때까지 반복
while q:
# 큐에서 원소 꺼내기
now = q.popleft()
# 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for i in graph[now]:
result[i] = max(result[i], result[now] + time[i])
indegree[i] -= 1
# 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if indegree[i] == 0:
q.append(i)
# 위상 정렬을 수행한 결과 출력
for i in range(1, v + 1):
print(result[i])
topology_sort()
'책 리뷰 > 이것이 취업을 위한 코딩테스트다' 카테고리의 다른 글
| 7일차 - 최단 경로 (1) | 2024.01.05 |
|---|---|
| 6일차 - 다이나믹 프로그래밍 (3) | 2024.01.04 |
| 5일차 - 이진 탐색 (1) | 2024.01.03 |
| 4일차 - 정렬 (0) | 2024.01.02 |
| 3일차 - DFS/BFS (1) | 2023.12.27 |





댓글 영역