고정 헤더 영역
상세 컨텐츠
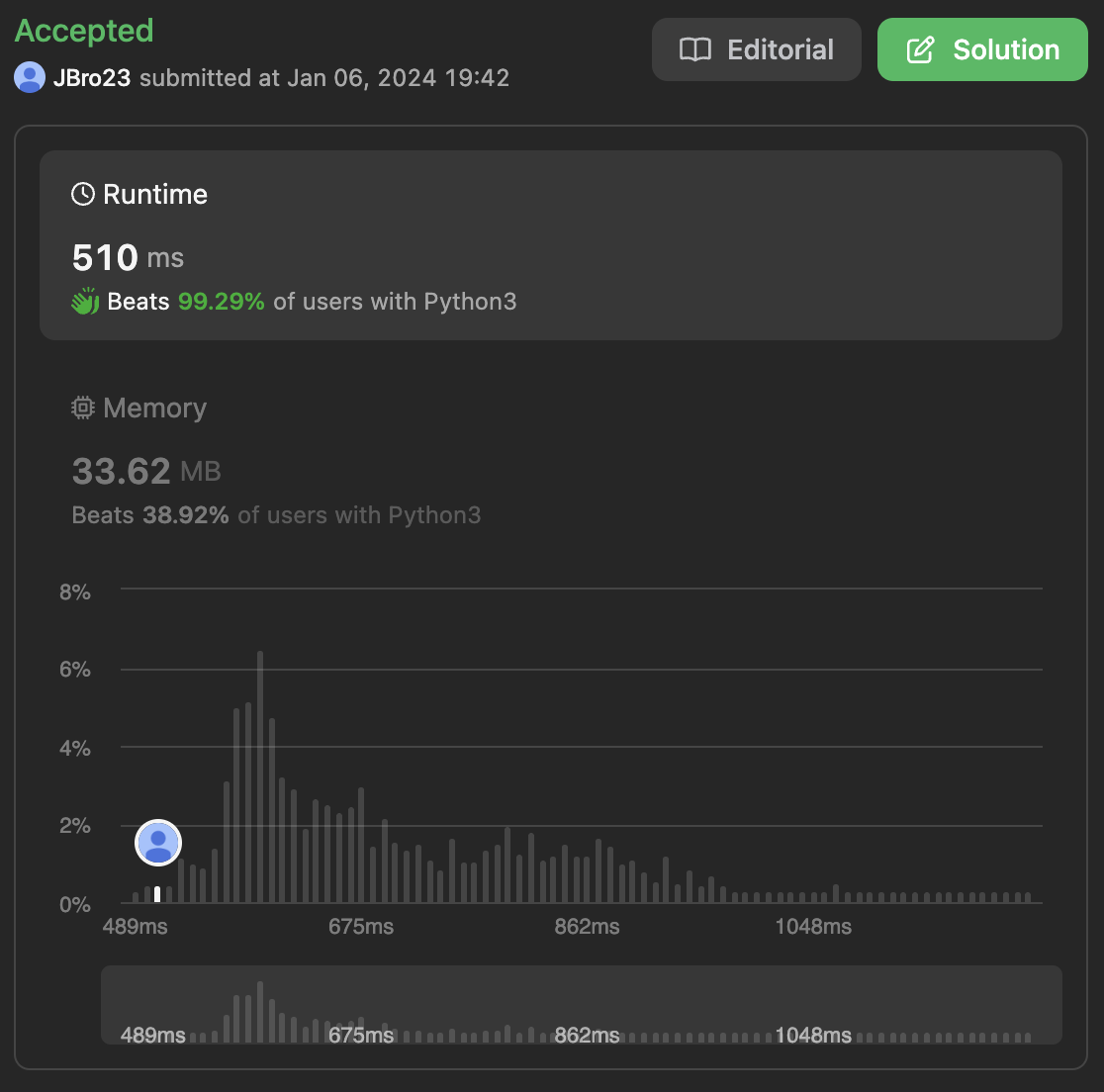
본문
Maximum Profit in Job Scheduling - LeetCode
Can you solve this real interview question? Maximum Profit in Job Scheduling - We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i]. You're given the startTime, endTime and profit arrays,
leetcode.com
일의 스케쥴이 주어지고, 스케쥴이 안겹치게 해서 최대한의 이득을 뽑는 문제이다.
이 문제는 우선순위 큐라고 생각이 들었다.
하지만 이코테 책 중 최단 경로를 공부하면서 파이썬은 우선순위 큐보다 힙큐의 수행시간이 훨씬 빠르다는 글을 보았다.
https://baseballgrammer.tistory.com/98
7일차 - 최단 경로
최단 경로 알고리즘은 말 그대로 가장 짧은 경로를 찾는 알고리즘이다. 이 책에서는 다익스트라, 프로이드 워셜 알고리즘이 빈도수가 높아 그 두개의 유형을 다룬다. 다익스트라 최단 경로 알고
baseballgrammer.tistory.com
heapq를 사용해보자.
class Solution:
def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
answer = 0
jobs = sorted(zip(startTime, endTime, profit))
heap = []
for start, end, prof in jobs:
while heap and start >= heap[0][0]:
answer = max(answer, heap[0][1])
heappop(heap)
combined_job = (end, prof + answer)
heappush(heap, combined_job)
heap.sort(reverse = True, key = lambda x:x[1])
return heap[0][1]이 문제에서 사용한 주요 문법은 크게 두가지이다.
1. zip
2. heapq
zip은 job의 수행시작시각, 수행종료시각, 수행 이익을 한 묶음으로 할 수 있는 간편한 함수이다.
앞으로도 종종 애용할 것 같다.
여기서 zip한 list를 반복문을 통해
최대값의 종료시각과 현재일의 시작시각을 비교해가며 heapq.heappus를 통해 경우의 수를 늘려간다.
경우의 수가 다 정리 되었다면, 그 중 최대값을 return 한다.
'공부' 카테고리의 다른 글
| [LeetCode][Python] 2225. Find Players With Zero or One Losses (0) | 2024.01.15 |
|---|---|
| [Programmers][Python] 프로세스 (1) | 2024.01.10 |
| [Programmers][Python] 캐시 (0) | 2024.01.05 |
| [LeetCode][Python]300. Longest Increasing Subsequence (1) | 2024.01.05 |
| [Programmers][Python] 의상 (0) | 2024.01.04 |





댓글 영역